2023-2024学年小学期中检测卷（1-5单元）人教版数学五年级下册（含解析）

Word文档版

学考宝(xuekaobao.com)友情提示：html格式不完整，如有需要请根据文末提示下载并进行二次校对Word文档。

2023-2024学年小学期中检测卷（1-5单元）
人教版数学五年级下册
学校:___________姓名：___________班级：___________考号：___________
题号 一 二 三 四 五 六 总分
得分
注意事项：
1．答题前填写好自己的姓名、班级、考号等信息
2．请将答案正确填写在答题卡上
一、选择题（10分）
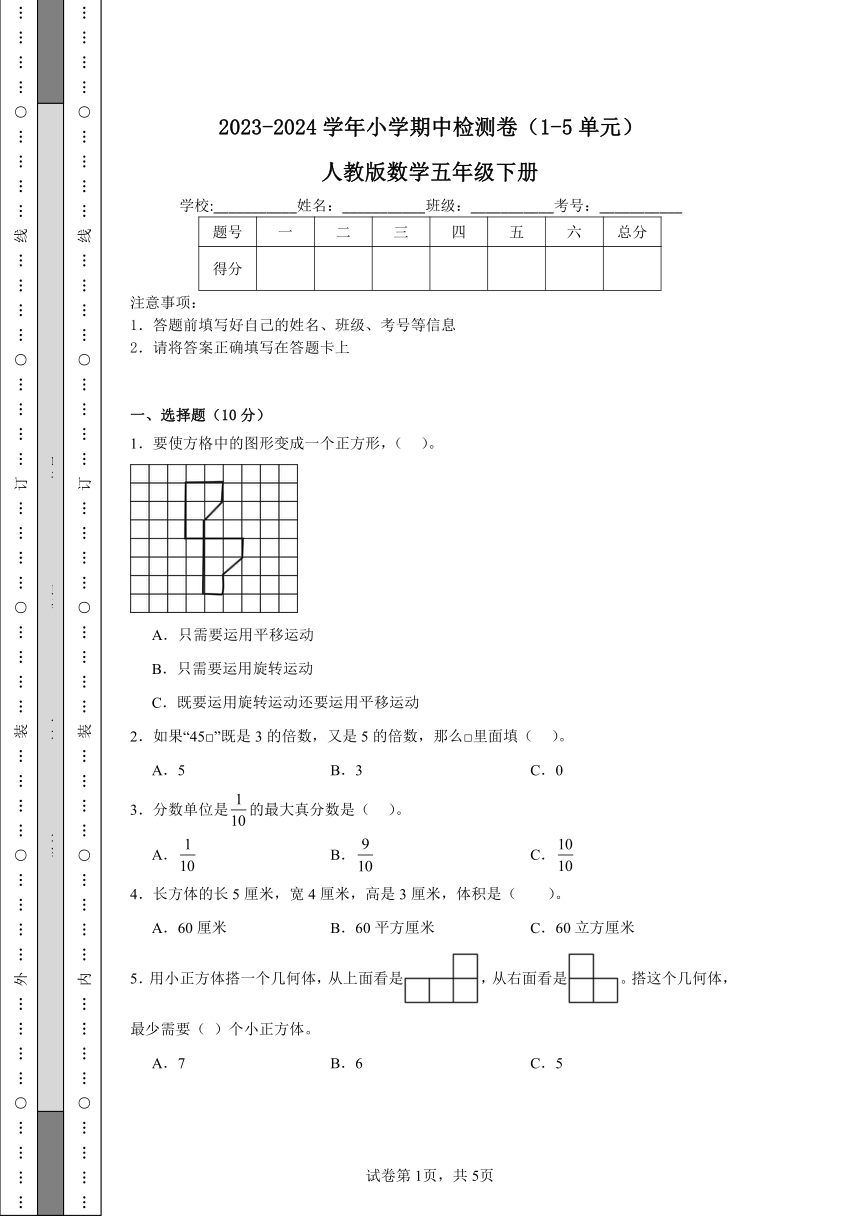
1．要使方格中的图形变成一个正方形，（ ）。
A．只需要运用平移运动
B．只需要运用旋转运动
C．既要运用旋转运动还要运用平移运动
2．如果“45□”既是3的倍数，又是5的倍数，那么□里面填（ ）。
A．5 B．3 C．0
3．分数单位是的最大真分数是（ ）。
A． B． C．
4．长方体的长5厘米，宽4厘米，高是3厘米，体积是（　　）。
A．60厘米 B．60平方厘米 C．60立方厘米
5．用小正方体搭一个几何体，从上面看是，从右面看是。搭这个几何体，最少需要（ ）个小正方体。
A．7 B．6 C．5
二、填空题（19分）
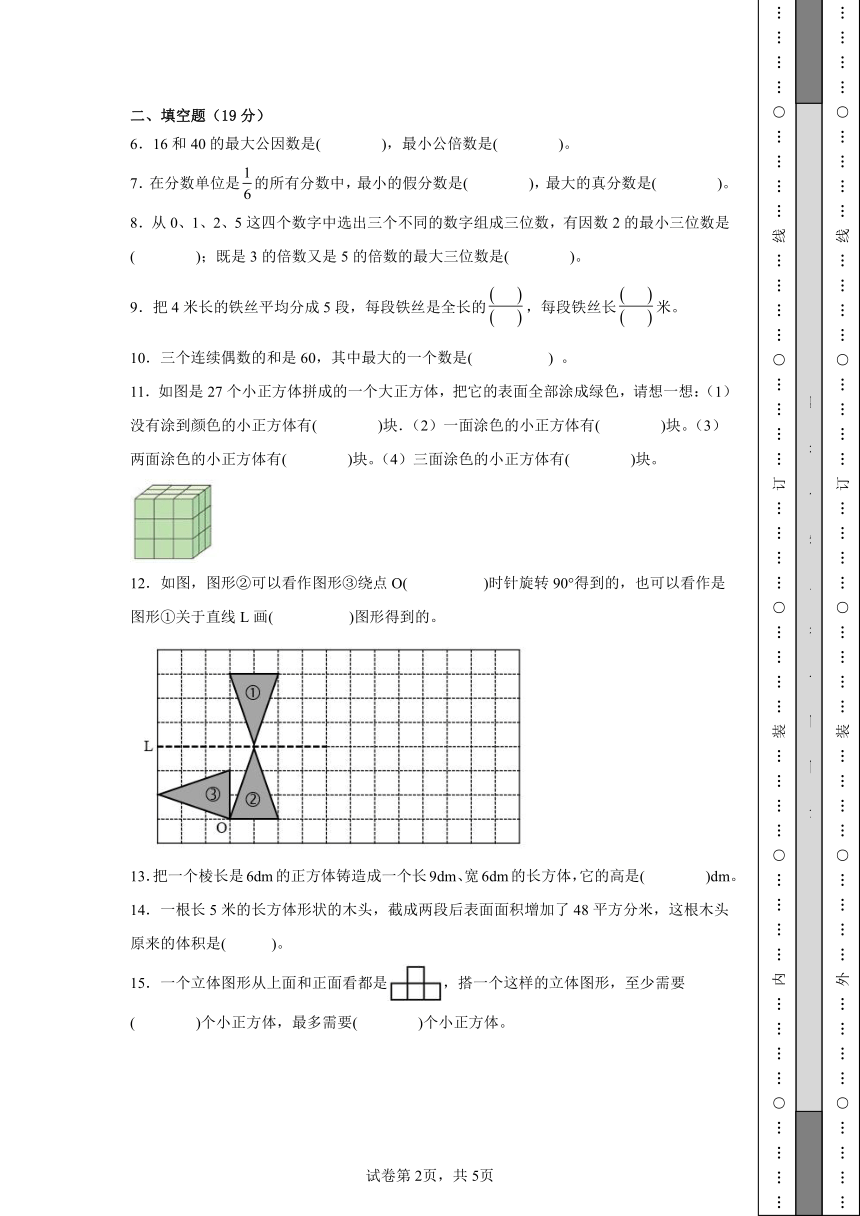
6．16和40的最大公因数是( )，最小公倍数是( )。
7．在分数单位是的所有分数中，最小的假分数是( )，最大的真分数是( )。
8．从0、1、2、5这四个数字中选出三个不同的数字组成三位数，有因数2的最小三位数是( )；既是3的倍数又是5的倍数的最大三位数是( )。
9．把4米长的铁丝平均分成5段，每段铁丝是全长的，每段铁丝长米。
10．三个连续偶数的和是60，其中最大的一个数是( ) 。
11．如图是27个小正方体拼成的一个大正方体，把它的表面全部涂成绿色，请想一想：（1）没有涂到颜色的小正方体有( )块．（2）一面涂色的小正方体有( )块。（3）两面涂色的小正方体有( )块。（4）三面涂色的小正方体有( )块。
12．如图，图形②可以看作图形③绕点O( )时针旋转90°得到的，也可以看作是图形①关于直线L画( )图形得到的。
13．把一个棱长是6dm的正方体铸造成一个长9dm、宽6dm的长方体，它的高是( )dm。
14．一根长5米的长方体形状的木头，截成两段后表面面积增加了48平方分米，这根木头原来的体积是( )。
15．一个立体图形从上面和正面看都是，搭一个这样的立体图形，至少需要( )个小正方体，最多需要( )个小正方体。
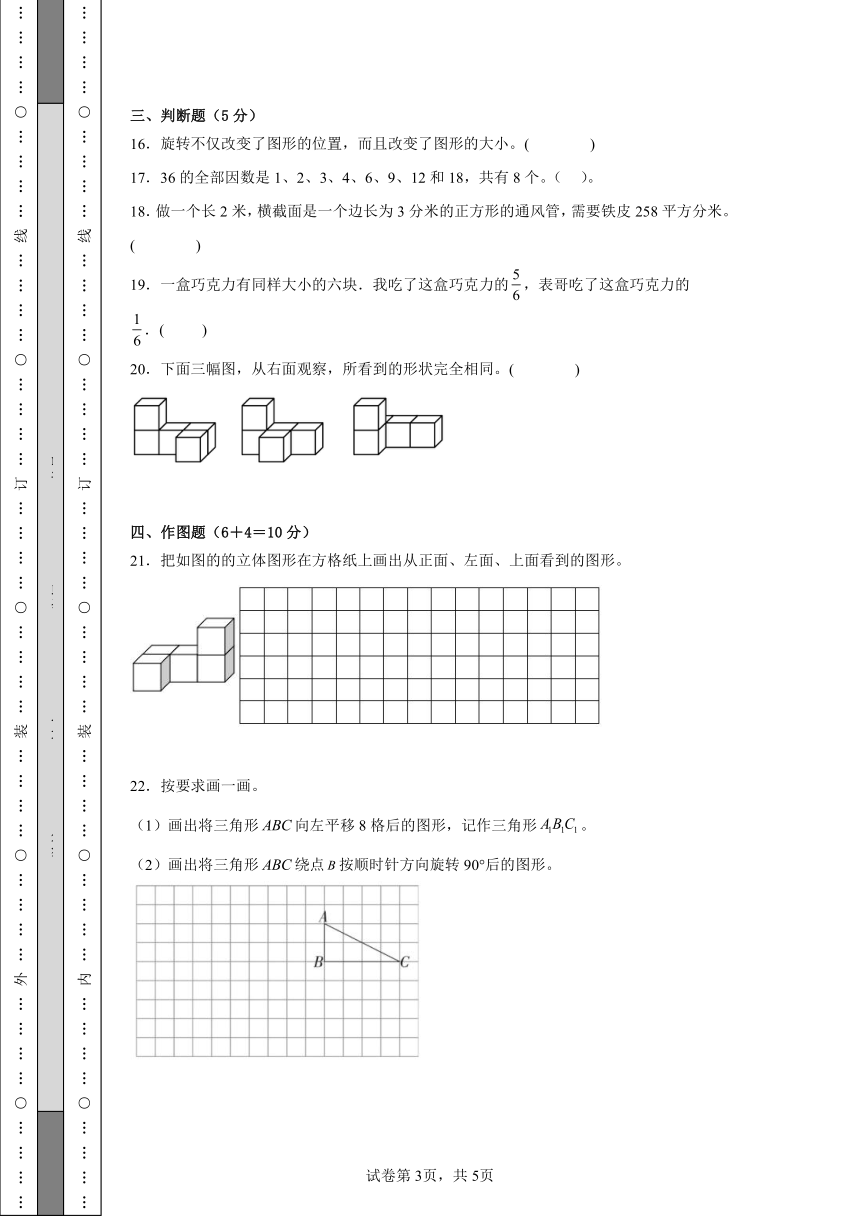
三、判断题（5分）
16．旋转不仅改变了图形的位置，而且改变了图形的大小。( )
17．36的全部因数是1、2、3、4、6、9、12和18，共有8个。（ ）。
18．做一个长2米，横截面是一个边长为3分米的正方形的通风管，需要铁皮258平方分米。( )
19．一盒巧克力有同样大小的六块．我吃了这盒巧克力的，表哥吃了这盒巧克力的．( )
20．下面三幅图，从右面观察，所看到的形状完全相同。( )
四、作图题（6＋4＝10分）
21．把如图的的立体图形在方格纸上画出从正面、左面、上面看到的图形。
22．按要求画一画。
（1）画出将三角形向左平移8格后的图形，记作三角形。
（2）画出将三角形绕点按顺时针方向旋转90°后的图形。
五、计算题（8＋5＋8＝21分）
23．写出下面每组数的最大公因数和最小公倍数。
①4和9 ②16和12 ③13和52 ④14和10
24．把下面的分数化成分母是10而大小不变的分数。
＝ ＝
25．计算下列图形的表面积和体积（单位：厘米）。
六、解答题（6*3＋8＋9＝35分）
26．一本科技书，小芳看了80页，还剩下40页没看。看过的页数占这本书总页数的几分之几？
27．48名学生排队，要求每行的人数相同，可以排成几行？有几种不同的排法，请分别写出来。（至少写出5种）
28．有两个正方体铁块，它们的表面积分别是24dm2和54dm2，现将这两个铁块熔铸成一个长方体铁块，铁块的宽是5dm，高是5cm，长是多少？
29．早锻炼时，爸爸发现路边有一排电线杆每相邻两根间的距离是45m，现在要改成60m，如果起点的那根不动，再隔多远又有一根不必移动？
30．有一个长方体玻璃鱼缸（如图），长8分米，宽7分米，高5分米，缸内水深4.5分米。如果将一块棱长为3分米的正方体铁块完全浸入水中，缸里的水会溢出来吗？请写出你的思考过程。
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名：___________班级：___________考号：___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
试卷第1页，共3页
试卷第1页，共3页
参考答案：
1．C
【分析】根据旋转和平移的特征，把下面的图形绕两个图形的连接点逆时针旋转180°后，再向右平移两格即可变成一个正方形。
【详解】要使方格中的图形变成一个正方形，既要运用旋转运动还要运用平移运动，
故答案为：C。
【点睛】掌握平移和旋转的特征与方法是解决此题的关键，平移：有上、下、左、右平移；旋转：逆时针旋转和顺时针旋转。
2．C
【分析】
5的倍数特征：个位数是0或5；3的倍数特征：各个数位上的数字和是3的倍数；据此解答。
【详解】要使“45□”是5的倍数，则个位数是能填0或5；
4＋5＋0＝9
4＋5＋5＝14
9是3的倍数，14不是3的倍数，所以450既是3的倍数，又是5的倍数，455只是5的倍数，不是3的倍数。□里面填0。
故答案为：C
3．B
【分析】根据分数单位的意义，把单位“1”平均分成若干份，表示其中1份的数叫分数单位。分数单位是的分数即分母是10的分数。根据真分数的意义，分子小于分母的分数是真分数，分数单位是的真分数的分子是的自然数，其中分子是9时最大，即分数单位是的最大真分数是。
【详解】分数单位是的最大真分数是。
故答案为：
【点睛】此题考查的知识点：分数单位的认识、真分数的意义、分数的大小比较。
4．C
【分析】根据长方体的体积＝长×宽×高，可计算出这个长方体的体积，因为这个长方体的长度单位是厘米，所以它的体积单位是立方厘米，列式解答即可得到答案。
【详解】5×4×3＝60（立方厘米）
这个长方体的体积是60立方厘米。
故答案为：C
【点睛】此题主要考查的是长方体的体积计算。
5．C
【分析】从上面看是，那么这个几何体的第一层至少有4个小正方体。从右面看是，那么第二层至少有1个小正方体。据此解题。
【详解】4＋1＝5（个）
所以，搭这个几何体，最少需要5个小正方体。
故答案为：C
【点睛】本题考查了物体三视图的认识，有一定空间观念是解题的关键。
6． 8 80
【分析】用短除法求两个数的最大公因数和最小公倍数，把这两个数写在短除号里面，除以它们的公有的质因数，一直除到所得的两个商互质，只有公因数1为止。把所有的除数相乘，就得到这两个数的最大公因数；把所有的除数和最后的两个商连乘起来，就得到两个数的最小公倍数。
【详解】
16和40的最大公因数是：2×2×2＝8
16和40的最小公倍数是：2×2×2×2×5＝80
【点睛】掌握求两个数的最大公因数和最小公倍数的方法是解题的关键。
7．
【分析】把单位“1”平均分成若干份，表示其中一份的数叫分数单位。
分子比分母小的分数叫做真分数。最大的真分数的分子比分母小1。
分子比分母大或分子和分母相等的分数叫做假分数。最小的假分数的分子与分母相等。
【详解】分数单位是的假分数有：、、、……；
分数单位是的真分数有：、、、、；
其中，最小的假分数是，最大的真分数是。
8． 102 510
【分析】2的倍数的特征：个位上是0、2、4、6、8的数；据此可知，有因数2的最小三位数的百位是1，十位是0，个位是2；
3、5倍数的特征：个位是0或5，并且各个数位之和能够被3整除；据此可知，既是3的倍数又是5的倍数的最大三位数的百位是5，个位则是0，十位只能是1，据此解答即可。
【详解】从0、1、2、5这四个数字中选出三个不同的数字组成三位数，有因数2的最小三位数是102；既是3的倍数又是5的倍数的最大三位数是510。
【点睛】熟练掌握2、3、5倍数的特征是解答本题的关键。
9．；
【分析】将铁丝长度看作单位“1”，求每段铁丝是全长的几分之几，用1÷段数；求每段长度，用铁丝长度÷段数。
【详解】1÷5＝
4÷5＝（米）
【点睛】分数的分子相当于被除数，分母相当于除数。
10．22
【分析】设中间的偶数为x，则这三个连续的偶数为x－2、x、x＋2，再根据三个连续偶数的和是60，列方程解答即可。
【详解】解：设中间的偶数为x，则这三个连续的偶数为x－2、x、x＋2；
x－2＋x＋x＋2＝60
3x＝60
x＝20
20＋2＝22；
【点睛】本题采用了方程的形式进行解答，明确三个连续偶数之间的关系是解答本题的关键。
11． 1 6 12 8
【详解】略
12． 顺 轴对称
【分析】由图可知，图形②在图形③的右边，图形③旋转到图形②点O的位置不变，对应边的夹角为90°，那么图形③绕旋转中心O按顺时针的方向旋转90°就可以得到图形②，将图形沿着一条直线对折，如果直线两侧的部分可以完全重合，这样的图形叫做轴对称图形，则图形①和图形②关于直线L对称，据此解答。
【详解】分析可知，图形②可以看作图形③绕点O顺时针旋转90°得到的，也可以看作是图形①关于直线L画轴对称图形得到的。
【点睛】本题主要考查旋转和轴对称的认识，旋转图形确定旋转中心、旋转方向、旋转角度是关键点。
13．4
【分析】把正方体铸造成长方体，只是形状变了，但是体积不变。根据正方体的体积公式：V＝a3，求出正方体的体积，用体积除以长方体的底面积即可求出长方体的高。
【详解】6×6×6÷（9×6）
＝216÷54
＝4（dm）
【点睛】解答此题关键是明白体积不变，再根据正方体和长方体的体积公式解答。
14．1200平方分米
【分析】把一根长5米的长方体形状的木头截成两段后，表面面积增加了48平方分米，表面积增加了2个横截面的面积，由此可以求得这根木头的横截面的面积为48÷2＝24平方分米，再利用长方体的体积公式即可解答。
【详解】5米＝50分米
48÷2×50
＝24×50
＝1200（平方分米）
【点睛】根据切割特点，利用增加的表面积求出长方体形状的木头的横截面的面积是解决本题的关键。
15． 5 6
【分析】一个立体图形从上面和正面看都是， 说明这个立体图形分为上下两层，下层有4个小正方体，上层至少有1个小正方体，所以这个立体图形至少有4＋1＝5个小正方体；上层最多有2个小正方体，所以这个立体图形最多需要4＋2＝6个小正方体。
【详解】根据分析可得：
最少：4＋1＝5（个）
最多：4＋2＝6（个）
故答案为：5；6。
【点睛】本题考查观察物体 ，解答本题的关键是根据从上面和正面看到的图形判断出这个立体图形有两层，且下层有4个小正方体。
16．×
【分析】旋转是物体绕着某一点或轴运动，本身方向发生了变化。根据旋转的特征可知，物体或图形旋转后，它们的形状、大小都不改变，只是位置发生了变化。据此解答。
【详解】根据分析得，旋转改变了图形的位置，但没有改变图形的形状和大小。所以原题的说法是错误的。
故答案为：×
【点睛】此题的解题关键是理解旋转的意义并掌握旋转的特征。
17．×
【分析】根据找一个数的因数的方法，进行列举，继而判断即可。
【详解】36的因数有1、2、3、4、6、9、12、18、36，共9个；
故答案为：×。
【点睛】解答此题应根据找一个数的因数的方法进行解答，注意找因数时要成对成对的找，防止遗漏。
18．×
【分析】根据题意，通风管无上下底，求出这个长方体的侧面积，就是这个通分管需要铁皮的面积，根据长方体侧面积公式：侧面积＝底面周长×高，代入数据，求出需要铁皮的面积，再进行比较，即可解答；注意单位名数的统一。
【详解】2米＝20分米
3×4×20
＝12×20
＝240（平方分米）
做一个长2米，横截面是一个边长为3分米的正方形的通风管，需要铁皮240平方分米。
原题干说法错误。
故答案为：×
19．√
【分析】1盒巧克力，分成同样大小的6份，一个吃了这盒巧克力的，一个吃了这盒巧克力的，这盒巧克力正好吃完，这是符合实际的，所以这种说法正确．
【详解】我吃了这盒巧克力的，表哥吃了这盒巧克力的，这盒巧克力分成了大小相等的六块，相当于我吃了5块，表哥吃了1块，正好吃完，这种说法是正确的．故答案为√．
20．×
【分析】观察物体，第一个从右面看会看到两层，下面一层2个小正方形，上面有1个小正方形右齐；第二个从右面看会看到两层，下面一层2个小正方形，上面有1个小正方形右齐，第三个从右面看会看到两层，下面一层2个小正方形，上面一层1个小正方形左齐，据此即可判断。
【详解】前两个物体的右视图为，第三个物体的右视图为，看到的形状不完全相同，原题说法错误。
故答案为：×
【点睛】此题考查学生的空间想象能力，能将视图画出是解题的关键。
21．见详解
【分析】这个立体图形由5个相同的小正方体组成。从正面能看到4个相同的小正方形，分两层，上层1个，下层3个，右对齐；从上面能看到4个相同的小正方形，分两层，上层3个，下层1个，左对齐；从左面能看到3个相同的小正方形，分两层，上层1个，下层2个，左对齐。
【详解】
【点睛】本题是考查作简单图形的三视图，能正确辨认从正面、上面、左面（或右面）观察到的简单几何体的平面图形。
22．见详解
【分析】（1）作平移后的图形步骤：找点－找出构成图形的关键点；定方向、距离－确定平移方向和平移距离；画线－过关键点沿平移方向画出平行线；定点－由平移的距离确定关键点平移后的对应点的位置；连点－连接对应点
（2）作旋转一定角度后的图形步骤：根据题目要求，确定旋转中心、旋转方向和旋转角；分析所作图形，找出构成图形的关键点；找出关键点的对应点：按一定的方向和角度分别作出各关键点的对应点；作出新图形，顺次连接作出的各点即可。
【详解】
【点睛】决定平移后图形的位置的要素：一是平移的方向，二是平移的距离。决定旋转后图形的位置的要素：一是旋转中心或轴，二是旋转方向（顺时针或逆时针），三是旋转角度。
23．①1；36
②4；48
③13；52
④2；70
【分析】①4和9是互质数，它们的最大公因数是1，最小公倍数是它们的乘积；②④根据这两个数的公有质因数的连乘积是这两个数的最大公因数，两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数解答；③因为52÷13＝4，当两个数成倍数关系时，较大的那个数是这两个数的最小公倍数，较小的那个数是这两个数的最大公因数；由此解答。
【详解】①4和9是互质数，它们的最大公因数是1，最小公倍数是4×9＝36；②16＝2×2×2×2，12＝2×2×3，所以16和12的最大公因数是：2×2＝4，16和12的最小公倍数是：2×2×2×2×3＝48；③13和52是倍数关系，最大公因数是13，最小公倍数是52；④14＝2×7，10＝2×5，所以14和10的最大公因数是2，14和10的最小公倍数是：2×5×7＝70。
【点睛】考查了求几个数的最大公因数的方法与最小公倍数的方法：两个数的公有质因数连乘积是最大公因数；两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数；数字大的可以用短除法解答。
24．；；；；；
【分析】根据分数的基本性质，分子和分母同时乘或除以一个不为0的数，分数的大小不变。
【详解】 ＝ ＝
25．表面积：1712平方厘米；体积：4320立方厘米
【分析】图中的几何体可以看成是从长、宽、高分别为20厘米、20厘米、12厘米的长方体上面切下一个长、宽、高分别为20厘米、6厘米、4厘米的小长方体，算表面积可以用平移的方法求解，最终相当于是原长方体的表面积减去两个的面，求体积直接用大长方体体积减去小长方体体积即可。
【详解】（厘米）
表面积：
（平方厘米）
体积：
（立方厘米）
26．
【分析】先用看过的页数加上剩下的页数，求出这本书的总页数，再用看过的页数除以总页数即可。注意计算结果能约分的要约成最简分数。
【详解】80÷（80＋40）
＝80÷120
＝
答：看过的页数占这本书总页数的。
【点睛】本题考查分数与除法的关系，明确求一个数占另一个数的几分之几，用除法计算。
27．详见解析
【分析】要求每行的人数相同，可以排成几行？即求48的因数，有：1、2、3、4、6、8、12、16、24、48；
如果每行1人，可以排48行；如果每行2人，可以排24行；如果每行3人，可以排16行；如果每行4人，可以排12行；如果每行6人，可以排8行；如果每行8人，可以排6行；如果每行12人，可以排4行；如果每行16人，可以排3行，如果每行24人，可以排2行，如果每行48人，可以排1行。
【详解】48＝1×48＝2×24＝3×16＝4×12＝6×8；
如果每行1人，可以排48行；如果每行2人，可以排24行；
如果每行3人，可以排16行；如果每行4人，可以排12行；
如果每行6人，可以排8行；如果每行8人，可以排6行；
如果每行12人，可以排4行；如果每行16人，可以排3行；
如果每行24人，可以排2行，如果每行48人，可以排1行。
【点睛】解答此题的关键：先根据找一个数的因数的方法，求出48的因数，进而根据题意，列举出所有的排法。
28．14分米
【分析】先根据正方体的表面积公式，求出两个正方体的棱长。因为两个正方体熔铸成一个长方体，体积不变。所以求出的两个正方体的体积之和就是长方体的体积，再根据长方体的体积公式求出长方体的长是多少。
【详解】5厘米＝0.5分米
24÷6＝4（平方分米），因为2的平方是4，所以这个正方体的棱长是2分米；
54÷6＝9（平方分米），因为3的平方是9，所以这个正方体的棱长是3分米。
（2×2×2＋3×3×3）÷（5×0.5）
＝（8＋27）÷2.5
＝35÷2.5
＝14（分米）
答：长方体的长是14分米。
【点睛】本题的关键是正方体熔铸成长方体，体积前后不变，然后根据长＝长方体体积÷宽÷高，计算出长。
29．
再隔3× 5× 3× 4=180(m)又有一根不必移动．
【详解】略
30．不会；思考过程见详解
【分析】根据题意，可知玻璃鱼缸没有水的高度为5－4.5＝0.5（分米），用8×7×0.5求出玻璃鱼缸空白部分的体积，再与铁块的体积比较。如果空白部分的体积大于等于铁块体积，水不会溢出；如果空白部分的体积小于铁块体积，水会溢出，据此解答即可。
【详解】5－4.5＝0.5（分米）
8×7×0.5
＝56×0.5
＝28（立方分米）
3×3×3＝27（立方分米）
28＞27，
答：缸里的水不会溢出来。
【点睛】解答本题的关键是先求出玻璃鱼缸没有水的部分的体积，再与铁块的体积进行比较。
答案第1页，共2页
答案第1页，共2页

图片资源预览