已知函数f(x)=x3(a>0且a≠1).(1)求函数f(x)的定义域;(2)讨论函数f(x)的奇偶性;...
已知函数f(x)=x3(a>0且a≠1).(1)求函数f(x)的定义域;(2)讨论函数f(x)的奇偶性;(3)求a的取值范围,使f(x)>0在定义域上恒成立.答案:解:(1)由于ax-1≠0,则ax≠1,所以x≠0,所以函数f(x)的定义域为{x|x∈R,且x≠0}.(2)对于定义域内任意的x,有f(-x)=(-x)3=-x3=-x3=x3=f(x),所以f(x)是偶函数.(3)①当a>1时,对x>0,所以ax>1,即ax-1>0,所以+>0.又x>0时,x3>0,所以x3>0,即当x>0时,f(x)>0.由(2)知,f(x)是偶



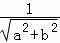
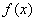



![函数的定义域为()A.(-3,0] B.(-3,1]C.(-∞,-3)∪(-3,0] D.(-...](https://static.xuekaobao.com/202405/lwd1rkjd6hia8.gif)
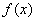
![对于实数x,符号[x]表示不超过x的最大整数,例如[π]=3,[﹣1.08]=﹣2,定义函数f(x)=x...](https://static.xuekaobao.com/202405/t9tkdypaz9h3t.gif)