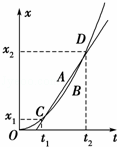
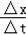如图所示，倾角为30°的光滑斜面与粗糙的水平面平滑连接．现将一滑块（可视为质点）从斜面上A点由静止释放，...
2024-04-29 08:52:52 学考宝 作者：佚名
题目
如图所示，倾角为30°的光滑斜面与粗糙的水平面平滑连接．现将一滑块（可视为质点）从斜面上A点由静止释放，最终停在水平面上的C点．已知A点距水平面的高度h=0.8m，B点距C点的距离L=2.0m．（滑块经过B点时没有能量损失，g=10m/s2），求：
（1）滑块在运动过程中的最大速度；
（2）滑块与水平面间的动摩擦因数μ；
（3）滑块从A点释放后，经过时间t=1.0s时速度的大小．
答案和解析
考点：
牛顿第二定律；匀变速直线运动的速度与时间的关系；匀变速直线运动的速度与位移的关系．
专题：
牛顿运动定律综合专题．
分析：
（1）滑块在斜面上时，对其受力分析，受到重力、支持力和摩擦力，根据牛顿第二定律列
式求解出加速度，再根据运动学公式计算末速度；
（2）对减速过程运用牛顿第二定律列式，再运用速度位移公式列式，最后联立方程组求解；
（3）先判断加速时间，再根据速度时间关系公式求解t=1.0s时速度的大小．
解答：
解：（1）滑块先在斜面上做匀加速运动，然后在水平面上做匀减速运动，故滑块运动到B点时速度最大为vm，设滑块在斜面上运动的加速度大小为a1
根据牛顿第二定律，有
mgsin30°=ma1
根据运动学公式，有
解得：vm=4m/s
即滑块在运动过程中的最大速度为4m/s．
（2）滑块在水平面上运动的加速度大小为a2
根据牛顿第二定律，有
μmg=ma2
根据运动学公式，有
vm2=2a2L
解得：μ=0.4
即滑块与水平面间的动摩擦因数μ为0.4．
（3）滑块在斜面上运动的时间为t1
根据运动学公式，有
vm=a1t1
得t1=0.8s
由于t＞t1，
故滑块已经经过B点，做匀减速运动t﹣t1=0.2s
设t=1.0s时速度大小为v
根据运动学公式，有
v=vm﹣a2（t﹣t1）
解得：v=3.2m/s
滑块从A点释放后，经过时间t=1.0s时速度的大小为3.2m/s．
点评：
本题关键先对滑块的加速和减速过程运用牛顿第二定律列式求解，再分别对两个过程运用运动学公式列方程联立求解．
